Why Isn't There a Replication Crisis in Math?

One important thing that I think about a lot, even though I have no formal expertise, is the replication crisis. A shocking fraction of published research in many fields, including medicine and psychology, is flatly wrong—the results of the studies can’t be obtained in the same way again, and the conclusions don’t hold up to further investigation. Medical researcher John Ioannidis brought this problem to wide attention in 2005 with a paper titled Why Most Published Research Findings Are False; attempts to replicate the results of major psychology papers suggest that only about half of them hold up. A recent analysis gives a similar result for cancer research.

This is a real crisis for the whole process of science. If we can’t rely on the results of famous, large, well-established studies, it’s hard to feel secure in any of our knowledge. It’s probably the most important problem facing the entire project of science right now.

There’s a lot to say about the mathematics we use in social science research, especially statistically, and how bad math feeds the replication crisis.¹ But I want to approach it from a different angle. Why doesn’t the field of mathematics have a replication crisis? And what does that tell us about other fields, that do?

Why doesn’t math have a replication crisis?

Maybe mathematicians don’t make mistakes

Have you, uh, met any mathematicians?

Comic by Ben Orlin at Math with Bad Drawings

At Caltech, they made the youngest non-math major split the check: the closer you were to high school, the more you remembered of basic arithmetic. But everyone knew the math majors were hopeless.

More seriously, it’s reasonably well-known among mathematicians that published math papers are full of errors. Many of them are eventually fixed, and most of the errors are in a deep sense “unimportant” mistakes. But the frequency with which proof formalization efforts find flaws in widely-accepted proofs suggests that there are plenty more errors in published papers that no one has noticed.

So math has, if not a replication crisis, at least a replication problem. Many of our published papers are flawed. But it doesn’t seem like we have a crisis.

Maybe our mistakes get caught

In the social sciences, replicating a paper is hard. You have to get new funding and run a new version of the same experiment. There’s a lot of dispute about how closely you need to replicate all the mechanics of the original experiment for it to “count” as a replication, and sometimes you can’t get a lot of the details you’d need to do it right—especially if the original authors aren’t feeling helpful.² And after all that work, people won’t even be impressed, because you didn’t do anything original!

But one of the distinctive things about math is that our papers aren’t just records of experiments we did elsewhere. In experimental sciences, the experiment is the “real work” and the paper is just a description of it. But in math, the paper, itself, is the “real work”. Our papers don’t describe everything we do, of course. There’s a lot of intellectual exploration and just straight-up messing around that doesn’t get written down anywhere. But the paper contains a (hopefully) complete version of the argument that we’ve constructed.

And that means that you can replicate a math paper by reading it. When I’ve served as a peer reviewer I’ve read the papers closely and checked all the steps of the proofs, and that means that I have replicated the results. And any time you want to use an argument from someone else’s paper, you have to work through the details, and that means you’re replicating it again.

The replication crisis is partly the discovery that many major social science results do not replicate. But it’s also the discovery that we hadn’t been trying to replicate them, and we really should have been. In the social sciences we fooled ourselves into thinking our foundation was stronger than it was, by never testing it. But in math we couldn’t avoid testing it.

Maybe the crisis is here, and we just haven’t noticed

As our mathematics gets more advanced and our results get more complicated, this replication process becomes harder: it takes more time, knowledge, and expertise to understand a single paper. If replication gets hard enough, we may fall into crisis. The crisis might even already be here; the problems in psychological and medical research existed for decades before they were widely appreciated.

There’s some fascinating work in using computer tools to formally verify proofs, but this is still a niche practice. In theory we are continually re-checking all our work, but in practice that’s inconsistent, so it’s hard to be sure how deep the problems run. (Especially since flawed papers don’t really get retracted and you pretty much have to talk to active researchers in a field to know which papers you can trust.)

But while this is a real possibility that people should take seriously, I’m skeptical that we’re in the middle of a true crisis of replicability.³ Many papers have errors, yes—but our major results generally hold up, even when the intermediate steps are wrong! Our errors can usually be fixed without really changing our conclusions.

Since our main conclusions hold up, we don’t need to fix any downstream papers that relied on those conclusions. We don’t need to substantially revise what we thought we knew. We don’t need to jettison entire fields of research, the way psychology had to abandon the literature on social priming. There are problems, to be sure, and we could always do better. But it’s not a crisis.

“Mysterious” intuition

But isn’t it…weird…that our results hold up when our methods don’t? How does that even work?

We get away with it becuase we can be right for the wrong reasons—we mostly only try to prove things that are basically true. Ben Kuhn tweeted a very accurate-feeling summary of the whole situation in this twitter thread:

[D]espite the fact that error-correction is really hard, publishing actually false results was quite rare because “people’s intuition about what’s true is mysteriously really good.” Because we mostly only try to prove true things, our conclusions are right even when our proofs are wrong.⁴

This can make it weirdly difficult to resolve disagreements about whether a proof is actually correct. In a recent example, Shinichi Mochizuki claims that he has proven the \(abc\) conjecture, while most mathematicians don’t believe his argument is valid. But everyone involved is pretty confident the \(abc\) conjecture is true; the disagreement is about whether the proof itself is good.

Circumstantial evidence isn’t enough to make mathematicians happy.

If we find a counterexample to \(abc\) then Mochizuki is clearly wrong, but so is everyone else. If we find a consensus proof of \(abc\), then Mochizuki’s conclusion is right, but that does very little to make his argument more convincing. He could, very easily, just be lucky.

But—Psychologists have intuition, too

A lot of psychology results that don’t replicate look a little different from this perspective. Does standing in a power pose for a few seconds make you feel more confident? Probably! It sure feels like it does (seriously, stand up and give it a try right now); and it would be weird if it made you feel worse. Does it affect you enough, for a long enough time, to matter much? Probably not. That would also be weird.

Amy Cuddy demonstrating a power pose.
Photo by Erik (HASH) Hersman from Orlando, CC BY 2.0, via Wikimedia Commons

The studies we’ve done, when analyzed properly, don’t show a clear, consistent, and measurable effect from a few seconds of power posing. But that’s what you’d expect, right? There’s probably an effect, but it should be too small to reasonably measure. And that’s totally consistent with everything we’ve found.

Amy Cuddy⁵ had the intuition that power posing would increase confidence, and set out to prove it—just like Mochizuki had the intuition that the \(abc\) conjecture was true, and set out to prove it. Mochizuki’s proof was bad, but his top-line conclusion was probably right because the \(abc\) conjecture is probably correct. And Cuddy’s studies were flawed, but her intuition at the start was probably right, so her top-line conclusion is probably true.

Well, sort of.

Defaulting to zero

Let’s turn Cuddy’s question around for a bit.⁶ What are the chances that power posing has exactly zero affect on your psychology? That would be extremely surprising. Most things you do affect your mindset at least a little.⁷

So our expectation should be: either power posing makes you a little more confident, or it makes you a little less confident. It also probably makes you either a little more friendly or a little less friendly, a little more or a little less experimental, a little more or a little less agreeable—an effect of exactly zero would be a surprise.

But for confidence specifically, it would also be kind of surprising if power posing made you feel less confident. So my default assumption is that power posing causes a small increase in confidence. And nominally, Cuddy’s research asked whether that default assumption is correct.

But that’s just not a great question. It doesn’t really matter if standing in a power pose makes you feel marginally better for five seconds. Not worth a book deal and a TED talk, and barely worth publishing. Cuddy’s research was interesting because it suggested the effect of power posing was not only positive, but large—enough to make a dramatic, usable impact over an extended period of time.

If Cuddy’s results were true, they would be both surprising and important. But that’s just another way of saying they’re probably not true.

Power and Precision

Notice: we’ve shifted to a new, different question. We started out asking “does power posing make you more confident”, but now we’re answering “how much more confident does power posing make you”. This is a better question, sure, but it’s different. And the statistical tools appropriate to the first question don’t really work for the new and better one.

Statistical hypothesis testing is designed to give a yes/no answer to “is this effect real”. Hypothesis testing is surprisingly complicated to actually explain correctly, and probably deserves an essay or two on its own.⁸

I swear this picture makes sense.
ROC_curves.svg: Sharprderivative work: נדב ס, CC BY-SA 4.0, via Wikimedia Commons

To wildly oversimplify, we measure something, and check if that measurement is so big that it’s unlikely to occur by chance. If yes, we conclude that there’s a real effect from whatever we’re studying. If not, we generally conclude that there’s no effect.

But what if the effect is real, but very small? With this method, we conclude the effect is real if our measurements are big enough. But if the effect is small, our measurements won’t be big. Our study might not have enough power to find the effect even if it is real.⁹

We could run a more powerful study and find evidence of smaller effects if we could make more precise measurements. This approach has worked really well in fields like physics and chemistry, and a lot of fundamental physical discoveries were driven by new technology that allowed the measurement of smaller effects. Galileo’s experiments with falling speeds required him to invent improved timekeeping methods, and Coulomb developed his inverse-square law after his torsion balance allowed him to precisely measure electromagnetic attraction. In the modern era, we built extremely sensitive measurement devices to try to measure gravity waves and detect the Higgs boson.

If power posing increases confidence by 1% for thirty seconds, that would actually be perfectly fine if we could measure confidence to within a hundredth of a percent on a second-to-second basis. But social psychology experiments just don’t work that way—at least, not with our current technology. There’s too much randomness and behavioral variation. Effects of that size just aren’t detectable.

This doesn’t have to be a problem! If we want to know “how big is the effect of power posing”, the answer is “too small to detect”. That’s a fine answer. It tells you that you shouldn’t build any complicated apparatus based on exploiting the power pose. (Or write entire books on how it can change your life.)

But the question we started with was “does power posing have an effect at all?”. If the effect is small, we might struggle to tell whether it’s real or not.

But we already know the answer!

Imagine you’re a psychologist researching power posing. You measure a small effect, which could just be due to chance. But you’re pretty sure that the effect is real; clearly you didn’t do a good enough job in your study! It’s probably not even worth publishing.

So you try again. Or someone else tries again. And eventually someone runs a study that does see a large effect. (Occasionally the large effect is due to fraud. Usually it’s methodology with subtler flaws that the researcher doesn’t notice. And sometimes it’s just luck: you’ll get a one-in-twenty outcome once in every twenty tries.)

Now we’re all happy. We were pretty sure that we would see an effect if we looked closely enough. And there it is! At this point no one has an incentive to look for flaws in the study. The result makes sense. (You might remember we said this is the state of a lot of mathematical research.)

But there are two major problems we can run into here. The first is that our intuition can, in fact, be wrong. If your process can only ever prove things that you already believed, it’s not a good process; you can’t really learn anything. Andrew Gelman recently made this observation about fraudulent medical research:

If you frame the situation as, “These drugs work, we just need the paperwork to get them approved, and who cares if we cut a few corners, even if a couple people die of unfortunate reactions to these drugs, they’re still saving thousands of lives,” then, sure, when you think of aggregate utility we shouldn’t worry too much about some fraud here and there…

But I don’t know that this optimistic framing is correct. I’m concerned that bad drugs are being approved instead of good drugs….Also, negative data—examples where the treatment fails to work as expected—provide valuable information, and by not doing real trials you’re depriving yourself of opportunities to get this feedback.

Shoddy research practices make sense if you see scientific studies purely as bureaucratic hoops you have to jump through: it’s “obviously true” that power posing will make you bolder and more confident, and the study is just a box you have to check before you can go around saying that out loud. But if you want to learn things, or be surprised by your data, you need to be more careful.

Effect Sizes Matter

Overestimation

The second problem can bite you even if your original intuition is right. You start out just wanting to know “is there an effect, y/n?”, but your experiment will make a measurement. You will get an estimate of the size of the effect. And that estimate will be wrong.

Your estimate will be wrong for a silly, almost tautological reason: if you can only detect large effects, then any effect you detect will be large. If you keep looking for an effect, over and over again, until finally one study gets lucky and sees it, that study will almost necessarily give a wild overestimate of the effect size.

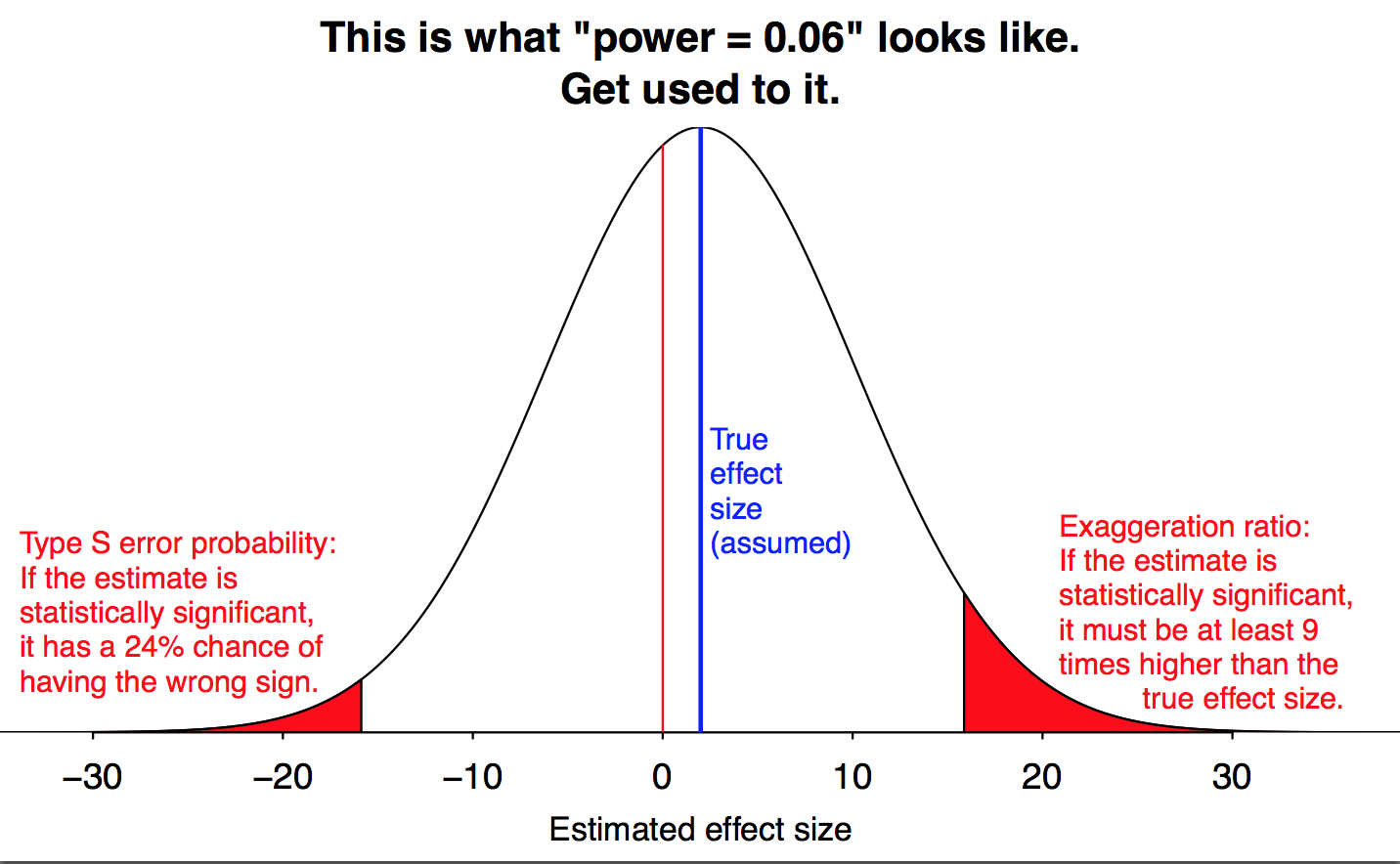
If the effect is small relative to your measurement precision, your results are guaranteed to be misleading. Figure by Andrew Gelman.

And this is how you wind up with shoddy research telling you that all sorts of things have shockingly large and dramatic impacts on…whatever you’re studying. You start out with the intuition that power posing should increase confidence, which is reasonable enough. You run studies, and eventually one of them agrees with you: power posing does make you more confident. But not just a little. In your study, people who did a little power posing saw big benefits.

To your surprise, you’ve discovered a life-changing innovation. You issue press releases, write a book, give a TED talk, spread the good news of how much you can benefit from this little tweak to your life.

Then other researchers try to probe the effect further—and it vanishes. Most studies don’t find clear evidence at all. The ones that do find something show much smaller effects than you had found. Of course they do. Your study had an unusually rare result, because that’s why it got published in the first place.

Don’t forget your prior

Notice how, in all of this, we lost sight of our original hypothesis. It seemed basically reasonable to think power posing might perk you up a bit. That’s what we originally wanted to test, and that’s the conviction that made us keep trying. But we didn’t start out thinking that it would have a huge, life-altering impact.

A really large result should feel just as weird as no result at all, if not weirder. And when we stop to think about that, we know it; some research suggests that social scientists have a pretty good idea which results are actually plausible, and which are nonsense overestimates But since we started with the question “is there an effect at all”, the large result we got feels like it confirms our original belief, even though it really doesn’t.

This specific combination is dangerous. The direction of the effect is reasonable and expected, so we accept the study as plausible. The size of the effect is shocking, which makes the study interesting, and gets news coverage and book deals and TED talks.

And this process repeats itself over and over, and the field builds up a huge library of incredible results that can’t possibly all be true. Eventually the music stops, and there’s a crisis, and that’s where we are today. But it all starts somewhere reasonable: with people trying to prove something that is obviously true.

So how is math different?

This is exactly the situation we said math was in. Mathematicians have pretty good idea of what results should be true; but so do psychologists! Mathematicians sometimes make mistakes, but since they’re mostly trying to prove true things, it all works out okay. Social scientists are also (generally) trying to prove true things, but it doesn’t work out nearly so well. Why not?

In math, a result that’s too good looks just as troubling as one that isn’t good enough. The idea of “proving too much” is a core tool for reasoning about mathematical arguments. It’s common to critique a proposed proof with something like “if that argument worked, it would prove all numbers are even, and we know that’s wrong”. This happens at all levels of math, whether you’re in college taking Intro to Proofs, or vetting a high-profile attempt to solve a major open problem. We’re in the habit of checking whether a result is—literally!—too good to be true.

We could bring a similar approach to social science research. Daniël Lakens uses this sort of argument to critique a famous study on hunger and judicial decisions:

I think we should dismiss this finding, simply because it is impossible. When we interpret how impossibly large the effect size is, anyone with even a modest understanding of psychology should be able to conclude that it is impossible that this data pattern is caused by a psychological mechanism. As psychologists, we shouldn’t teach or cite this finding, nor use it in policy decisions as an example of psychological bias in decision making.

Other researchers have found specific problems with the study, but Lakens’s point is that we could dismiss the result even before they did. If a proposed proof of Fermat’s last theorem also shows there are no solutions to $a^2 + b^2 = c^2$, we know it’s wrong, even before we find the specific flaw in the argument. And if a study suggest humans aren’t capable of making reasoned decisions at 11:30 AM, it’s confounded by something, even if we don’t know what.

And yet, while I don’t believe in these studies, and I don’t believe their effect sizes, I still believe their basic claims. I believe that people make worse decisions when they’re hungry. (I know I do.) I believe standing in a power pose can make you feel stronger and more assertive. I believe that exercising self-control can deplete your willpower.

But as a mathematician, I’m forced to admit: we don’t have proof.

Do you think we have a replication crisis in math? Disagree with me about the replication crisis? Think you make better decisions when you’re hungry? Tweet me @ProfJayDaigle or leave a comment below.